Rubin, T. & Panaretos V. M. (2020). Sparsely Observed Functional Time Series: Estimation and Prediction. Electronic Journal of Statistics, 14 (1): 1137-1210, 2020
arXiv preprint: arxiv.org/abs/1811.06340
Software: The code used in the analyses together with my follow-up paper “Functional Lagged Regression with Sparse Noisy Observations” is available on GitHub:
https://github.com/tomasrubin/sparse-functional-lagged-regression
Nontechnical summary:
This paper constitutes the core result of my PhD dissertation. I developed a novel method for the analysis of time series data consisting of sparsely observed smooth curves, i.e. we assume existence of unobserved “platonic” curves (Theory picture in the following figure) ordered in time that are sampled only at a low number of locations with possible noise contamination (Practise picture).

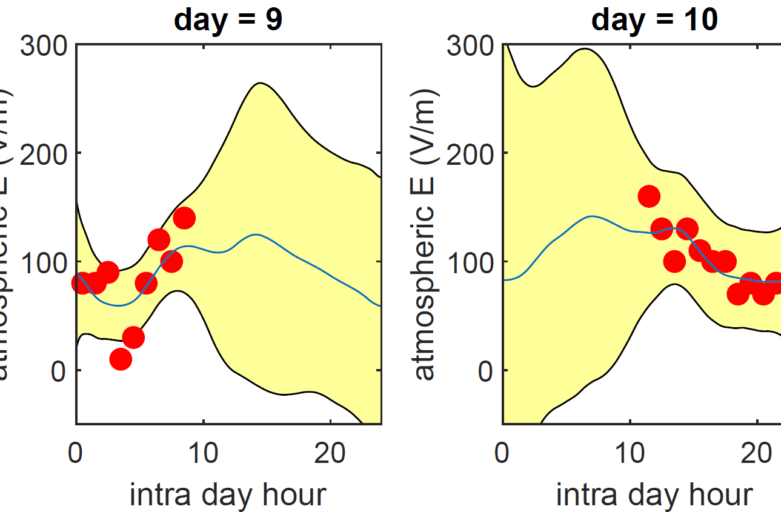
An example of such data and the data I analysed in the paper is the atmospheric electric conductivity measured in Tashkent, Uzbekistan. The time series is segmented into days and the conductivity evolution within each day is considered to be the “platonic” curve, the functional datum. The problem is that this variable is measured only under the so-called fair-weather conditions and thus the measurements are sparsely and irregularly scattered (red points in the figure bellow, corresponding to the crosses above in the Practice picture). The primarily objective is to recover the unobserved “platonic” curves (the blue curves, i.e. the fair-weather atmospheric electricity), and quantify the uncertainty (the yellow bands) brom the observation (the red points) without any parametric assumptions.

The method provides also with interpretation of the data dynamics, such as within- and inter-day behaviour, and periodicity (some visualisation below).
What are the implications of this paper?
My method does not assume any parametric model and constitutes the first non-parametric approach for such data. The removal of parametric assumptions provides with flexible method that is adaptive to any underlying truth (subject to some very general assumptions) and thus can provide arguments for a choice of more rigid models. Moreover it provides framework for my follow-up research, Rubin and Panaretos (2020), Rubin (2020).
Abstract:
Functional time series analysis, whether based on time or frequency domain methodology, has traditionally been carried out under the assumption of complete observation of the constituent series of curves, assumed stationary. Nevertheless, as is often the case with independent functional data, it may well happen that the data available to the analyst are not the actual sequence of curves, but relatively few and noisy measurements per curve, potentially at different locations in each curve’s domain. Under this sparse sampling regime, neither the established estimators of the time series’ dynamics nor their corresponding theoretical analysis will apply. The subject of this paper is to tackle the problem of estimating the dynamics and of recovering the latent process of smooth curves in the sparse regime. Assuming smoothness of the latent curves, we construct a consistent nonparametric estimator of the series’ spectral density operator and use it to develop a frequency-domain recovery approach, that predicts the latent curve at a given time by borrowing strength from the (estimated) dynamic correlations in the series across time. This new methodology is seen to comprehensively outperform a naive recovery approach that would ignore temporal dependence and use only methodology employed in the i.i.d. setting and hinging on the lag zero covariance. Further to predicting the latent curves from their noisy point samples, the method fills in gaps in the sequence (curves nowhere sampled), denoises the data, and serves as a basis for forecasting. Means of providing corresponding confidence bands are also investigated. A simulation study interestingly suggests that sparse observation for a longer time period may provide better performance than dense observation for a shorter period, in the presence of smoothness. The methodology is further illustrated by application to an environmental data set on fair-weather atmospheric electricity, which naturally leads to a sparse functional time series.