Masak, Rubin, Panaretos (2022). Inference and Computation for Sparsely Sampled Random Surfaces. Journal of Computational and Graphical Statistics, 31:4, 1361-1374,
Non-technical description:
- We developed a general method how to analyse data composed of points observed on surfaces. The method estimates the correlation structure of the data without parametric assumptions, predicts the unobserved surfaces, and constructs confidence bands.
- Under the assumption of separability, our method enjoys massive computational gains (tens of seconds versus hours).
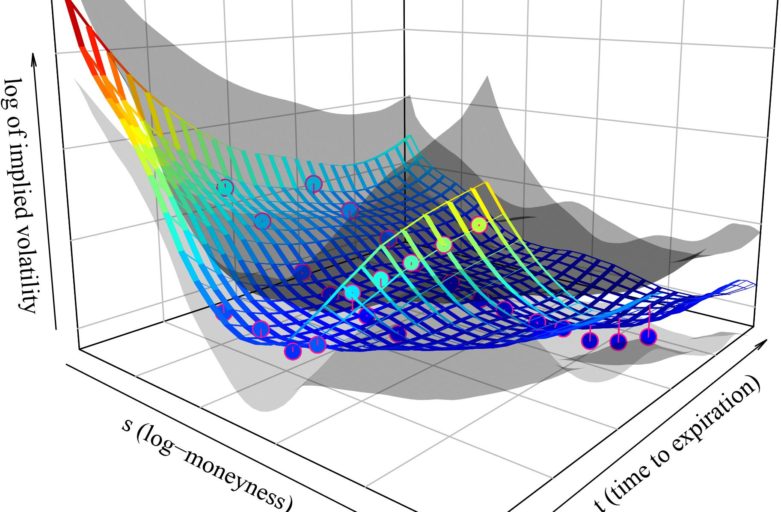
- We applied our method to implied volatility (IV) surfaces data where the implied volatilities are calculated from the call options on various stocks and equity indexes.
- Our method “borrows strength” across the entire data set in order to probe one IV surface. In other words, to predict/interpolate the IV surface of AAPL from just a few quoted/traded IVs corresponding to the calls on this stock, the our method looks into all other symbols like GOOGL, TSLA, etc. to learn how a typical IV surface looks like (estimating the correlation structure), an predicts/interpolates the AAPL surface.
- We showed that this “borrowing strength” leads to the interpolation error decrease of around 10 % over the benchmark that interpolates each IV surface individually.
Abstract:
Non-parametric inference for functional data over two-dimensional domains entails additional computational and statistical challenges, compared to the one-dimensional case. Separability of the covariance is commonly assumed to address these issues in the densely observed regime. Instead, we consider the sparse regime, where the latent surfaces are observed only at few irregular locations with additive measurement error, and propose an estimator of covariance based on local linear smoothers. Consequently, the assumption of separability reduces the intrinsically four-dimensional smoothing problem into several two-dimensional smoothers and allows the proposed estimator to retain the classical minimax-optimal convergence rate for two-dimensional smoothers. Even when separability fails to hold, imposing it can be still advantageous as a form of regularization. A simulation study reveals a favorable bias-variance trade-off and massive speed-ups achieved by our approach. Finally, the proposed methodology is used for qualitative analysis of implied volatility surfaces corresponding to call options, and for prediction of the latent surfaces based on information from the entire data set, allowing for uncertainty quantification. Our cross-validated out-of-sample quantitative results show that the proposed methodology outperforms the common approach of pre-smoothing every implied volatility surface separately.